Quasicrystals
Quasicrystals
Quasicrystals form in alloys of
aluminum with transition metals such as iron or copper. They are
distinguished by their novel symmetries, such as the rotational
symmetry of an icosahedron, that are forbidden in crystalline
structures. Although lacking translational periodicity, quasicrystals
display translational quasiperiodicity, leading to the dense
collection of Bragg peaks in the diffraction pattern shown at the
left. Widespread commercialization of quasicrystals awaits discovery
of uses for these materials which display unusual hardness and
brittleness, low coefficients of friction, and high thermal and
electrical resistance. Some proposed applications include
wear-resistant surface treatments for other metals in ball bearings
and frying pans.
Research in the group of Michael
Widom at Carnegie Mellon focusses on understanding the structure and
thermodynamics of quasicrystalline alloys. Popular structural models
of quasicrystals invoke Penrose tilings like the one shown at the left
(taken from the
WWW
site of Hillman) that covers the plane with fat and thin rhombi
according to a set of "matching rules" that force a particular aperiodic
structure. Diffraction from such structures is nicely described in a
web site maintained by Lifshitz. Widom has shown that randomly tiling the
plane with the same set of shapes spontaneously generates structures
of appropriate symmetry and quasiperiodicity. The configuational
entropy of tiling the plane at random may help explain thermodynamic
stability of real quasicrystalline alloys.
Current research in abstract tiling
theory examines tilings of high rotational symmetry in collaboration
with Remy Mosseri and co-workers. Possibly the limit of high
rotational symmetry may prove easier to analyze than specific finite
symmetries (10-fold, for example) of direct physical interest.
Surprisingly, rhombus tilings are related to algorithms for sorting of
lists. Counting the number of distinct tilings enumerates
simultaneously the number of equivalance classes of sorting
algorithms, a problem previously considered by computer scientist
D.E. Knuth. Our random tiling theory implies an upper bound of
log(2) for the tiling entropy per vertex, consistent with a conjecture
by Knuth. Click here for a preprint on this
research. The figure above displays one particular rhombus tiling from
an ensemble of 18-fold rotational symmetry. The tiling (left)
corresponds (examine color coding of tiles and crossings of lines) to
the bubble sort on 9 element lists (right).
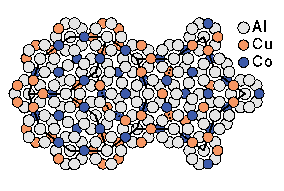In addition to research on
tilings, Widom collaborates with others on the problem of atomic
modeling of quasicrystal structures. This includes testing interatomic
potentials calculated by John Moriarty (Livermore National Lab) for
aluminum-rich intermetallic alloys, and performing ab-initio total
energy calculations utilizing density functional programs such as VASP
and LSMS together with Nassrin Moghadam (Oad Ridge National Lab) and
Yang Wang (Pittsburgh Supercomputer Center). These are applied to
realistic atomic structures in collaboration with Eric Cockayne
(NIST), Chris Henley (Cornell) and Marek Mihalkovic (Chemnitz).
Typical atomic configurations of decagonal quasicrystals are generated
by Monte Carlo simulations. Structures that resulted inspired the
model of decagonal AlCoCu shown at the left. Papers and posters
describing this work are available on the web.
Back to Widom research group page