A. Local rotation matrices

Local rotation matrices are used to rotate the global coordinate system (given by the definition of the Bravais matrix) to a local coordinate system for each atomic site. They are used in the program for two reasons:

• to minimize the number of LM combinations in the lattice harmonics expansion (of potential and charge density according to equ. 2.10). For example for point group mm2 one needs for L=1 just LM=1,0 if the coordinate system is chosen such that the z-axis coincides with the 2-fold rotation axis, while in an arbitrary coordinate system the three terms 1,0; 1,1 and -1,1 are needed (and so on for higher L).

• The interpretation e.g. of the partial charges requires a proper orientation of the coordinate system. In the example given above, the p orbitals split into 2 irreducible representations, but they can be attributed to $p_z$ and $p_x$, $p_y$ only if the z-axis is the 2-fold rotation axis.

It is of course possible to perform calculations without ``local rotation matrices``, but in such a case the LM combinations given in Table 7.42 (and by SYMMETRY) may not be correct. (The LM values for arbitrary orientations may be obtained from a procedure described in Singh 94.)

Fortunately, the ``local rotation matrices`` are usually fairly simple and are now automatically inserted into your case.struct file. Nevertheless we recommend to check them in order to be sure.

The most common coordinate transformations are

• interchanging of two axes (e.g. x and z)
• rotation by $45^\circ$ (e.g. in the xy-plane)
• rotation of z into the (111) direction

Inspection of the output of SYMMETRY tells you if the local rotation matrix is the unit matrix or it gives you a clear indication how to find the proper matrix.

The local rotation matrix $\mathbf R$ , which transforms the global coordinates $r$ to the rotated ones $r'$, is defined by $\mathbf R r = r'$.

There are two simple ways to check the local rotation matrixes together with the selected LM combinations:

• charge density plots generated with LAPW5 must be continuous across the atomic sphere boundary (especially valence or difference density plots are very sensitive, see 8.6)

• Perform a run of LAPW1 and LAPW2 using the GAMMA-point only (or a complete star of another k point). In such a case, ``wrong`` LM combinations must vanish. Note that the latter is true only in this case. For a k mesh in the IBZ ``wrong`` LM combinations do not vanish and thus must be omitted!!

A first example for ``local rotation matrices`` is given for the rutile TiO2, which has already been described as an example in section 10.3. Also two other examples will be given (see below).

1 Rutile ($TiO_2$)

Examine the output from symmetry. It should be obvious that you need local rotation matrices for both, Ti and O:

   ....
   Titanium   operation #  1     1                   
   Titanium   operation #  2     -1                  
   Titanium   operation #  5     2 || z              
   Titanium   operation #  6     m n z             
   Titanium   operation # 12     m n 110             
   Titanium   operation # 13     m n -110            
   Titanium   operation # 18     2 || 110            
   Titanium   operation # 19     2 || -110           
     pointgroup is mmm (neg. iatnr!!)
     axes should be: m n z, m n y, m n x

This output tells you, that for Ti a mirror plan normal to z is present, but the mirror planes normal to x and y are missing. Instead, they are normal to the (110) plane and thus you need to rotate x, y by $45^\circ$ around the z axis. (The required choice of the coordinate system for mmm symmetry is also given in Table 7.42)

   ....
   Oxygen     operation #  1     1                   
   Oxygen     operation #  6     m n z             
   Oxygen     operation # 13     m n -110            
   Oxygen     operation # 18     2 || 110            
     pointgroup is mm2 (neg. iatnr!!)
     axes should be: 2 || z, m n y

For O the 2-fold symmetry axes points into the (110) direction instead of z. The appropriate rotation matrices for Ti and O are:

$$\left ( \begin{array}{ccc} \frac{1}{\sqrt 2} & \frac {1}... ...t 2} & \frac {1}{\sqrt 2}\\ 1 & 0 & 0 \end{array} \right )$$

2 Si $\Gamma$-phonon

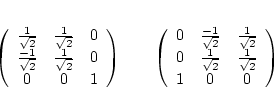
Si possesses a face-centered cubic structure with two equivalent atoms per unit cell, at ($\pm$0.125, $\pm$0.125, $\pm$0.125). The site symmetry is -43m. For the $\Gamma$-phnon the two atoms are displaced in opposite direction along the (111) direction and cubic symmetry is lost. The output of SYMMETRY gives the following information:

Si         operation #  1     1                   
Si         operation # 13     m n -110            
Si         operation # 16     m n -101            
Si         operation # 17     m n 0-11            
Si         operation # 24     3 || 111            
Si         operation # 38     3 || 111            
  pointgroup is 3m (neg. iatnr!!)
     axis should be: 3 || z, m n y
lm: 0 0  1 0  2 0  3 0  3 3  4 0  4 3  5 0  5 3  6 0  6 3  6

Therefore the required local rotation matrix should rotate z into the (111) direction and thus the matrix in the ``struct`` file should be:

0.4082483 -.7071068 0.5773503	$\frac{\sqrt 6}{6}$	$-\frac{\sqrt 2}{2}$	$\frac{\sqrt 3}{3}$
0.4082483 0.7071068 0.5773503	$\frac{\sqrt 6}{6}$	$\frac{\sqrt 2}{2}$	$\frac{\sqrt 3}{3}$
-.8164966 0.0000000 0.5773503	$-2\frac{\sqrt 6}{6}$	$\frac{\sqrt 2}{2}$	$\frac{\sqrt 3}{3}$

3 Trigonal Selenium

Selenium possesses space group P3121 with the following struct file:

H    LATTICE,NONEQUIV.ATOMS: 1
MODE OF CALC=RELA  POINTGROUP:32      
 8.2500000 8.2500000  9.369000
ATOM= -1: X= .7746000  Y= .7746000  Z= 0.0000000
          MULT= 3          ISPLIT= 8
ATOM= -1: X= .2254000  Y= .0000000  Z= 0.3333333
ATOM= -1: X= .0000000  Y= .2254000  Z= 0.6666667
Se         NPT=  381  R0=.000100000 RMT=2.100000000  Z:34.0
LOCAL ROT.MATRIX:    0.0       0.5000000 0.8660254
                     0.0000000 -.8660254 0.5000000
                     1.0000000 0.0000000 0.0
   6    IORD OF GROUP G0
......

The output of SYMMETRY reads:

Se         operation #  1     1                   
Se         operation #  9     2 $|$$|$ 110            
  pointgroup is 2 (neg. iatnr!!)
  axis should be: 2 || z
lm: 0 0  1 0  2 0  2 2 -2 2  3 0  3 2 -3 2  4 0  4 2 -4 2 ......

Point group 2 should have its 2-fold rotation axis along z, so the local rotation matrix can be constructed in two steps: firstly interchange x and z (that leads to z $\parallel$ (011) ) and secondly rotate from (011) into (001) (see the struct file given above). Since this is a hexagonal lattice, SYMMETRY uses the hexagonal axes, but the local rotation matrix must be given in cartesian coordinates.